How To Calculate Horizontal Tangent

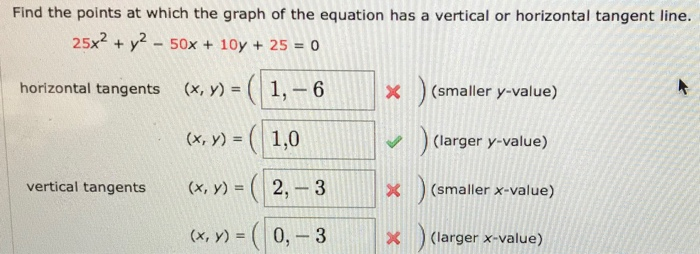
In this problem the differentiation has already been done, in "implicit" form - that is, both x and y occur in the function. Set the numerator to zero to find where the slope is horizontal, and set the denominator to zero to find vertical tangents. Knowing only the derivative, you will not be able to specify the actual point - just one of its two coordinates. A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. This is because, by definition, the derivative gives the slope of the tangent line. Therefore, when the derivative is zero, the tangent line is horizontal.

To find horizontal tangent lines, use the derivative of the function to locate the zeros and plug them back into the original equation. Horizontal tangent lines are important in calculus because they indicate local maximum or minimum points in the original function. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus. A horizontal tangent is parallel to x-axis and hence its slope is zero. We know that the slope is nothing but the derivative of the function.

So to find the points where there are horizontal tangents just set the derivative of the function to zero and solve. After getting the points, we can find the equation of the horizontal tangent line using the point-slope form. Determine the \(x\)-\(y\) coordinates of the points where the following parametric equations will have horizontal or vertical tangents.

We'll also look at where to find vertical tangent lines, and where to find horizontal tangent lines, since that's something you'll be asked to do often. Horizontal tangent lines exist where the derivative of the function is equal to 0, and vertical tangent lines exist where the derivative of the function is undefined. The formulas above fail when the point is a singular point. In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point. A vertical tangent is parallel to y-axis and hence its slope is undefined.

As the slope is nothing but the derivative of the function, to find the points where there are vertical tangents, see where the derivative of the function becomes undefined . After getting the points, we can find the equation of the vertical tangent line using the point-slope form. The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. Sketch the curves over the interval $[0,2\pi]$ unless otherwise stated. Use the first and second derivative to identify horizontal and vertical tangents and local maximum and minimum points.

Find the derivative using the rules of differentiation. Substitute the \(x\)-coordinate of the given point into the derivative to calculate the gradient of the tangent. Substitute the gradient of the tangent and the coordinates of the given point into an appropriate form of the straight line equation. The graph of z1 shown in Lesson 13.1 suggests that one branch of the curve has a horizontal tangent at and another branch has a vertical tangent at . This calculus video tutorial explains how to find the point where the graph has a horizontal tangent line using derivatives. You need to know the slope of a horizontal tangent line is zero.

You need to find the first derivative, set it equal to zero, and solve for x which may involve factoring a trinomial. The next topic that we need to discuss in this section is that of horizontal and vertical tangents. We can easily identify where these will occur (or at least the \(t\)'s that will give them) by looking at the derivative formula.

The tangent plane to a surface at a given point p is defined in an analogous way to the tangent line in the case of curves. The tangent at A is the limit when point B approximates or tends to A. Unlike a straight line, a curve's slope constantly changes as you move along the graph.

To find the equation for the tangent, you'll need to know how to take the derivative of the original equation. Find where the graph has vertical and horizontal tangent lines. Once you have the slope of the tangent line, which will be a function of x, you can find the exact slope at specific points along the graph. A horizontal tangent line is parallel to the x-axis and shows where a function has a slope of zero. You can find these lines either by looking at a graph or by setting an equation to zero to find maximums and minimums.

Differentiate the equation of the circle and plug in the values of x,y in the derivative. Use the slope-point form of the line to find the equation, with the slope you obtained earlier and the coordinates of the point. To plot polar coordinates, set up the polar plane by drawing a dot labeled "O" on your graph at your point of origin. Draw a horizontal line to the right to set up the polar axis. When you look at the polar coordinate, the first number is the radius of a circle. To plot the coordinate, draw a circle centered on point O with that radius.

Use a straight edge to verify that the tangent line points straight up and down at that point. Test the point by plugging it into the formula . If the right-hand side of the equation differs from the left-hand side , then there is a vertical tangent line at that point.

The study of curves can be performed directly in polar coordinates without transition to the Cartesian system. Find the equations of the horizontal tangent lines. In addition to finding the area under a parametric curve, we sometimes need to find the arc length of a parametric curve. In the case of a line segment, arc length is the same as the distance between the endpoints. If a particle travels from point A to point B along a curve, then the distance that particle travels is the arc length.

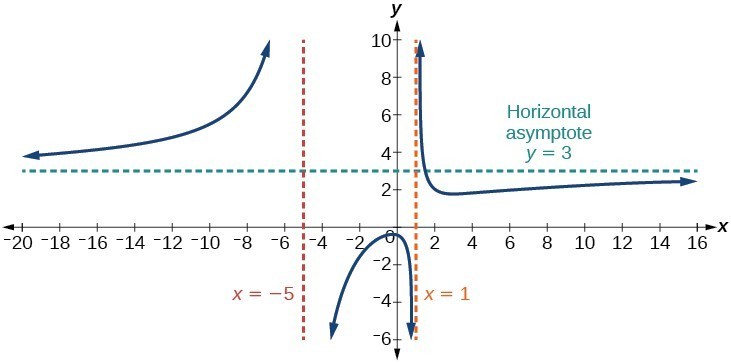
To develop a formula for arc length, we start with an approximation by line segments as shown in the following graph. These points correspond to the sides, top, and bottom of the circle that is represented by the parametric equations (Figure 1.19). On the left and right edges of the circle, the derivative is undefined, and on the top and bottom, the derivative equals zero. Knowing the slopes of tangent lines at various points on the graph of a function can help one better understand the graph of the overall function.

2) Plug x value of the indicated point into f ' to find the slope at x. 3) Plug x value into f to find the y coordinate of the tangent point. 4) Combine the slope from step 2 and point from step 3 using the point-slope formula to. To find a horizontal tangent, you must find a point at which the slope of a curve is zero, which takes about 10 minutes when using a calculator. Determine whether or not it has any maximums or minimums, also known as extrema. The tangent line of a curve at a given point is a line that just touches the curve at that point.

The tangent line in calculus may touch the curve at any other point and it also may cross the graph at some other point as well. If a line passes through two points of the curve but it doesn't touch the curve at either of the points then it is NOT a tangent line of the curve at each of the two points. In that case, the line is called a secant line.

Here, we can see some examples of tangent lines and secant lines. Let us see how to find the slope and equation of the tangent line along with a few solved examples. Also, let us see the steps to find the equation of the tangent line of a parametric curve and a polar curve. The "tangent line" is one of the most important applications of differentiation. The word "tangent" comes from the Latin word "tangere" which means "to touch".

The tangent line touches the curve at a point on the curve. So to find the tangent line equation, we need to know the equation of the curve and the point at which the tangent is drawn. The point at which the tangent is drawn is known as the "point of tangency". We can see the tangent of a circle drawn here.

Note that where functions have vertical tangent lines, they are not differentiable at that point. Vertical tangent lines occur at the points (-4, -1) and (2, -1). No, the curve cannot have a horizontal tangent where it crosses the x-axis. 2) Plug x value of the indicated point into f ' to find the slope at x. 4) Combine the slope from step 2 and point from step 3 using the point-slope formula to find the equation for the tangent line.

In mathematics, particularly calculus, a vertical tangent is a tangent line that is vertical. Because a vertical line has infinite slope, a function whose graph has a vertical tangent is not differentiable at the point of tangency. The vertical tangent to a curve occurs at a point where the slope is undefined .

This can also be explained in terms of calculus when the derivative at a point is undefined. If both the numerator and denominator of the formula for dy/dx are zero, the tangent at that point can be horizontal, vertical, or neither, and the only way to tell is by looking at the limit. Newton's method (also called the Newton–Raphson method) is a way to find x-intercepts of functions. In other words, you want to know where the function crosses the x-axis. The method works well when you can't use other methods to find zeros of functions, usually because you just don't have all the information you need to use easier methods. While Newton's method might look complex, all you're actually doing is finding a tangent line, then another tangent line, and repeat, until you think you're close enough to the actual solution.

Points Where Tangent Line Is Horizontal Calculator At which there are vertical and horizontal tangents. These methods led to the development of differential calculus in the 17th century. Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz. To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope.

Enter the x value of the point you're investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. So in this sense, calling it a tangent line seems reasonable. However, the red line also intersects the curve in two places, which suggests the reverse if we adhere to the old geometric definition of a tangent line. Understanding the nature of slopes of tangent lines to functions can raise red flags when appropriate to alert us to not be so quick to believe what we see on our calculator screens.

The tangent line equation calculator is used to calculate the equation of tangent line to a curve at a given abscissa point with stages calculation. This video contains a few examples and practice problems. A vertical line is a line, parallel to y-axis and goes straight, up and down, in a coordinate plane.

Whereas the horizontal line is parallel to x-axis and goes straight, left and right. Find a value of x that makes dy/dx infinite; you're looking for an infinite slope, so the vertical tangent of the curve is a vertical line at this value of x. To find the points at which the tangent line is horizontal, we have to find where the slope of the function is 0 because a horizontal line's slope is 0. Now set it equal to 0 and solve for x to find the x values at which the tangent line is horizontal to given function.

When you go back to your calculus next time, I would recommend double-checking with your teacher. But I know for a fact that setting the derivative equal to zero gets you a horizontal tangent. To find the specific coordinates, we can plug back into our parametric equations like before. Well, recall from your Calculus I class that with the second derivative we can determine where a curve is concave up and concave down. We could do the same thing with parametric equations if we wanted to.

A tangent is a line that intersects a curve at only one point and does not pass through it, such that its slope is equal to the curve's slope at that point. For the following exercises, each set of parametric equations represents a line. Without eliminating the parameter, find the slope of each line. Substitute the gradient of the normal and the coordinates of the given point into the gradient-point form of the straight line equation. Substitute the gradient of the tangent and the coordinates of the point into the gradient-point form of the straight line equation.

Substitute the gradient of the tangent and the coordinates of the given point into the gradient-point form of the straight line equation. The angle between two curves at a point where they intersect is defined as the angle between their tangent lines at that point. More specifically, two curves are said to be tangent at a point if they have the same tangent at a point, and orthogonal if their tangent lines are orthogonal.

At most points, the tangent touches the curve without crossing it . A point where the tangent crosses the curve is called an inflection point. Tangent line calculator is a free online tool that gives the slope and the equation of the tangent line. BYJU'S online tangent line calculator tool makes the calculations faster and easier where it displays the output in a fraction of seconds.

Suppose that the $x$-axis now represents time, and the $y$-axis represents the position/height of some object -- perhaps a rising red balloon. The slope of the tangent line is then a distance traveled divided by an elapsed time and can thus be interpreted as a velocity. It is possible from the equation of the representative curve of a function to use the online graphing calculator for draw the tangent of a function at a point. A vertical line has undefined slope because all points on the line have the same x-coordinate. As a result the formula used for slope has a denominator of 0, which makes the slope undefined.. Tangent, in geometry, straight line that touches a given curve at one point; at that point the slope of the curve is equal to that of the tangent.

A tangent line may be considered the limiting position of a secant line as the two points at which it crosses the curve approach one another. Tangent, in geometry, the tangent line to a curve at a point is that straight line that best approximates (or "clings to") the curve near that point. It may be considered the limiting position of straight lines passing through the given point and a nearby point of the curve as the second point approaches the first.